Nano. Lett. | 多层扭转银纳米线组装体及其结构相关的手性光学性质

今天与大家分享一篇发表在Nano Letters上的文章，标题是“多层扭转的银纳米线组装体及其结构相关的手性光学性质”。本文的通讯作者为法国斯特拉斯堡大学，查尔斯·萨德隆研究所的Matthias Pauly教授。

手性等离子体超表面的光学特性很大程度上依赖于它们的结构，特别是组装成大阵列时单个构建模块的取向及模块间距。另一方面，制备得到能够在跨越紫外、可见及近红外范围的具有手性光学特性且可精确调控的的手性超材料的方法是极少的。在这一工作中，作者通过掠入射喷涂技术和层层组装工艺将银纳米线（AgNW）制备成多层扭转结构，该多层手性复合材料设计原理简单，并且能够在一个较宽的波长范围内精确调控其手性光学性质。定向纳米线层之间的偏转角度决定了材料的圆二色性（CD）强度，其椭圆度值达到13°以上并且g因子值高达1.6。而CD光谱的峰形和峰位取决于AgNW的层间距离，并且层间距离是可以在纳米尺度范围进行调整的。最后，还利用基于转移矩阵的计算法成功模拟了材料结构相关的光学特性。

在本文中，作者首先将定向排列的AgNW层逐层组装，层与层之间扭转一定角度(α)，并利用介电聚合物控制AgNW层间距离，从而获得杂化手性等离子组装体。具体步骤如图1所示：首先，底层的定向AgNWs层是通过将银纳米线悬浮液掠入射喷涂沉积在预先涂有聚电解质的基底上获得的（图1a），流动液体的剪切流动诱导了AgNWs的定向沉积，导致单层纳米线定向排列并展现出各向异性的光学性质。其次，利用交替地沉积相反电荷的聚电解质(PEI/(PSS/PAH)_n/PSS/PEI)，形成一定厚度的聚合物层来控制AgNWs层间距离（d）（图1b）。最后，将整个基底旋转一定角度(α)，喷涂第二个定向AgNWs层（图1c）。在这一研究工作中，作者只进行了由不同旋转角度α及不同层间距d所组装的双层AgNWs材料的研究分析，但材料本身的设计是可以基于多层AgNWs的组装，或是利用其它一维纳米材料进行相同工艺的组装。

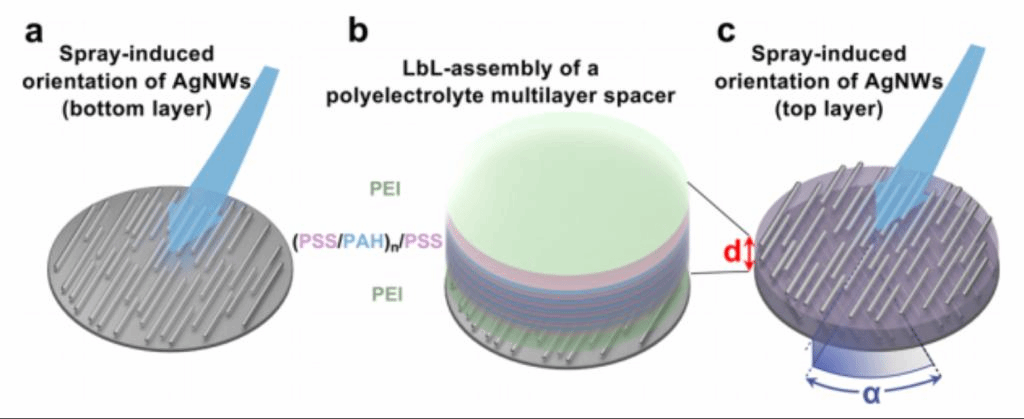
图1、样品的制备过程示意图。(a) 第一层定向银纳米线（AgNWs；d≈60 nm；L≈3-5 μm）通过喷涂在PEI涂层衬底上。(b) 通过聚电解质的层层组装得到可精确调节厚度的多层介电间隔层（PEI/（PSS/PAH）n/PSS/PEI）。(c) 最后，样品可以旋转任意角度(α)，进而在顶层沉积定向AgNW。

接下来，作者研究了AgNW层间角α对材料手性光学性质的具体影响。作者制备了一系列固定层间距为13 nm，层间角度不同（0°~90°）的双层AgNW结构材料，SEM图像能够清楚的看到单层定向排列的AgNW以及不同层间角度的双层AgNW样品（图2a）。根据角度α的正负（例如：+45°，-45°表示上层相对于下层顺时针或逆时针旋转45°），制备得到了左手或右手的扭转双层结构，从而得到对称的CD光谱。当α为0°或90°时，样品CD值接近于0，此时为非手性（外消旋）构型，而当α为45°时，CD值最大（图2b）。还利用椭圆度值及相应的转换公式计算得到了材料的g因子，结果表明，量化手性光学各向异性的g因子在α=45°和385 nm波长时达到最大值0.3。如图2c所示，将波长λ = 385和800 nm的g因子作为角度α的函数绘制了散点图，表现出随角度先增大后减小的趋势，这一函数变化规律对于其他波长也适用。此外，还利用Berreman转移矩阵法模拟了不同堆叠角度（α）的双层手性组装体的穆勒矩阵，并由此计算其CD。测量的CD通过模拟得到很好地再现，当α=0°或90°时计算得到的CD=0mdeg，当α=45°时的CD最大，并且对应峰的位置也得到了很好的对应。如图2d所示，CD强度的极坐标光谱是中心对称的，因为α和α+180°代表相同的结构，对于α和−α的对映体结构，其CD具有相同的光谱形状，但符号相反。

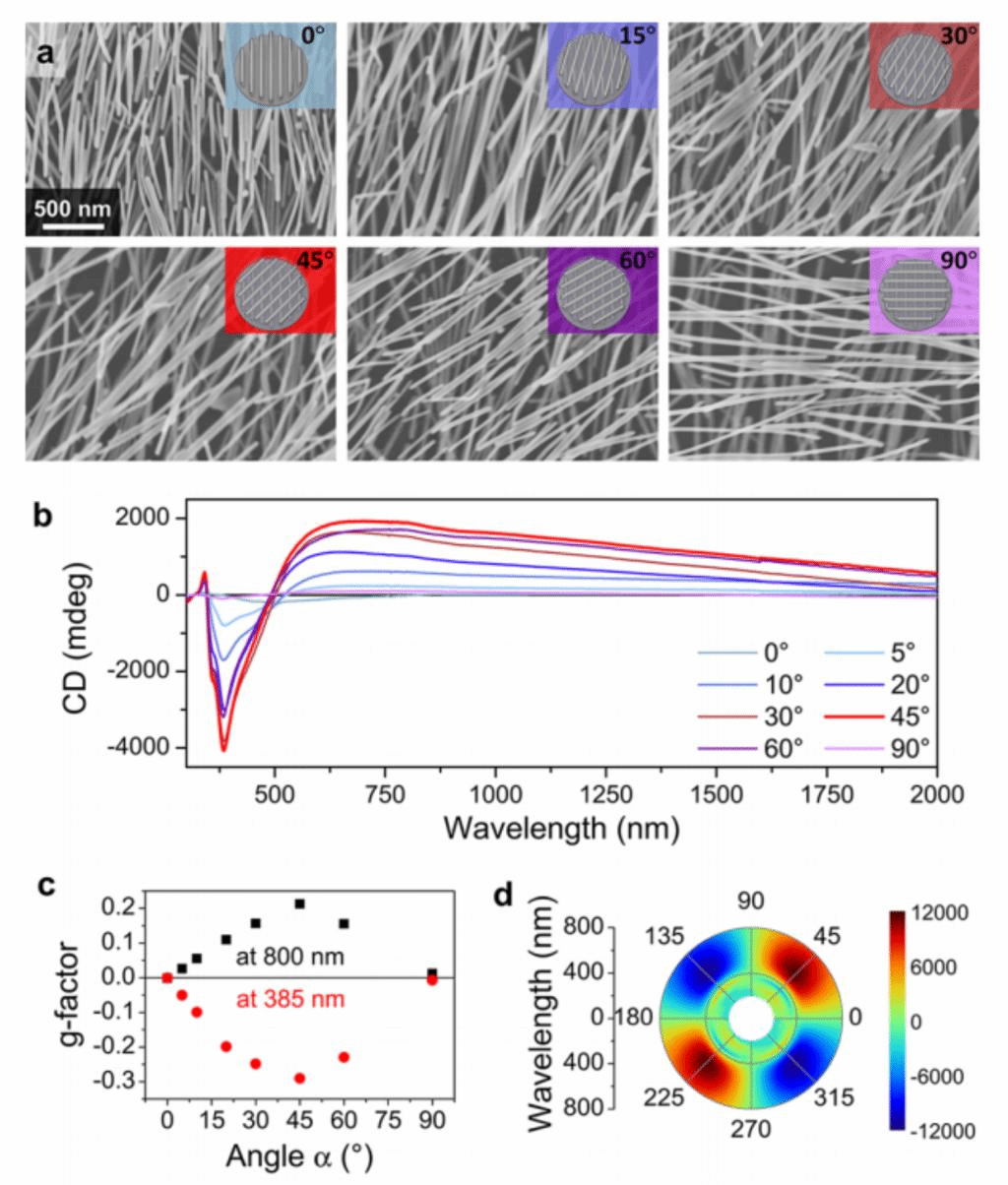
图2、不同层间角度(α)的双层AgNW样品的(a) SEM图像。（固定层间间距为13 nm）。以及(b)在UV−vis−NIR范围内测量得到的CD光谱。(c) 根据CD光谱计算了在385和800 nm处的g因子与α的关系图像。(d)固定层间距为13 nm，改变堆叠角度，模拟得到的材料光谱数据。图中半径对应波长，角坐标对应AgNW层之间的角α，颜色刻度为CD值。 

随后，作者将层间角度α固定为45°，研究不同的层间距离d对材料的光学性能的影响。LBL组装方式的独特优势之一在于能够在纳米尺度范围精确调整两层AgNWs之间的多层聚电解质厚度，从而控制AgNWs的层间距。图3a展示了不同层间距d的双层AgNWs结构的横截面扫描电镜图像。间距与PSS/PAH的层对数n成正比（图3b），每个聚电解质层对的厚度为2.1 nm。测定并计算了不同层间距d的双层AgNWs结构的CD及g因子谱图（图3c），结果发现，层间间距对薄膜CD的影响是显著的：位于385 nm处的负CD峰保持不变，但在可见光范围内的CD峰位随着层间距离的增加而发生红移，当层间距d≥100 nm时，g因子和CD光谱上出现振荡，并达到非常高的值。特别是在λ = 1500 nm下，d = 200 nm时CD > 13 000 mdeg，而此时薄膜的消光率只有0.25，因此g因子也达到1.6以上。这一极高的g因子值也达到了迄今为止报道的最高值，但这一由两层等离子体所组成的结构体系却要简单很多。而随着间距的增加，振荡周期越来越小，甚至在层间距离达到几微米的样品中也可以观察到同样的趋势。这一特征与“法珀腔”（Fabry Perot cavities）透射光谱中观察到的干涉非常相似，事实上，如果界面上的反射被抑制，或者聚合物层的相干性消失，这些振荡就会消失，CD光谱就会变得与间距无关。这也证实了CD光谱在大间距下的类干涉振荡是由纳米线层的反射及其各向异性响应所引起的。此外，作者还使用转移矩阵方法建模得到了CD，并与测量的CD结果较好的吻合，包括光谱可见光范围内峰的红移和较大层间距下的振荡（图3d）。

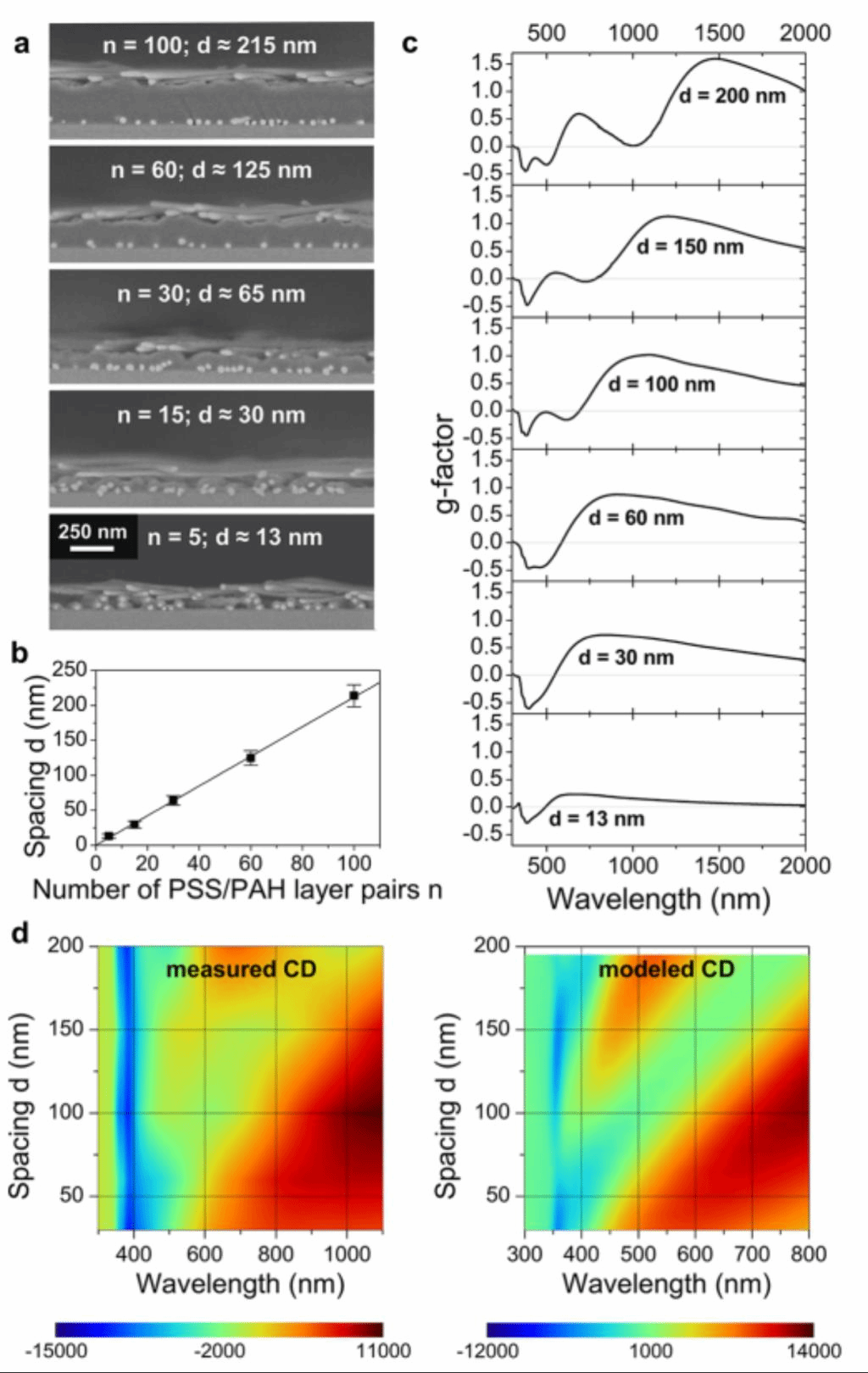
图3、(a) 具有不同层间距d的双层AgNW结构样品的横截面扫描电镜图像。(b) 层间距d与PSS/PAH层数n的关系曲线。(c) 随着层间距d的增加时材料的g因子谱图变化。(d) 测量（左）和模拟（右）CD光谱作为层间距d的函数。

总的来说，作者展示了一种结合掠入射喷涂技术和LBL方法制备的双层AgNWs手性等离子体复合薄膜。其中的聚电解质层可以控制AgNWs的层间距。其CD信号跨越了UV-vis-NIR区域，并且其手性光学性质可以通过改变双层AgNWs的层间扭转角度及层间距离进行精确调控。材料的CD强度直接取决于AgNW层间的夹角，当两层AgNWs间的夹角为45°时，获得最强的CD信号，而当夹角为0°或90°时，为非手性（外消旋）构型，CD信号为0。最终这一手性组装体的CD强度达到了超过13°这一极高的数值，其对应的g因子也达到了1.6。CD光谱中峰的位置强烈地依赖于AgNW层之间的间距，随层间距的增加，CD光谱中可见及NIR范围内的峰发生红移，当层间距进一步增大（>100 nm）时，这一范围内的峰还出现振荡现象，这些是由于在AgNW/聚合物界面上与偏振相关的反射所带来的干扰效应。作者还利用转移矩阵计算模拟了该材料的手性光学性质，与实验测量结果相匹配。

文字 郗盼毅

审核 叶曦翀

参考文献：DOI: 10.1021/acs.nanolett.1c02812

https://pubs.acs.org/doi/10.1021/acs.nanolett.1c02812